Matlab Assignment 1

Brett Roberts
September 26, 2006

Part 1

Question 4
T700 = 268.57 K, T500 = 251.92 K (U.S. standard atmosphere)
Tavg = (268.57 K + 251.92 K) / 2 = 260.25 K

Hypsometric Equation:
z2 - z1 = (Rd/g) * Tavg * ln(P1/P2)
Thickness = [(287 J K-1 kg-1) / (9.8 m s2)] * (260.25 K) * ln[(700 hPa) / (500 hPa)]
Thickness = 2564.5 m

Question 5
z700 = 3012.18 m, z500 = 5574.43 m (U.S. standard atmosphere)

Thickness = 5574.43 m - 3012.18 m = 2562.3 m

The difference in height given by the hypsometric equation is slightly different than that given by the U.S. Standard Atmosphere calculation. This is to be expected because the temperature used for the hypsometric calculation is a simple average of the two levels, while the standard atmosphere is based on more accurate calculations. Also, the hypsometric equation uses actual heights, whereas the standard atmosphere uses geopotential heights.


Figure 1:
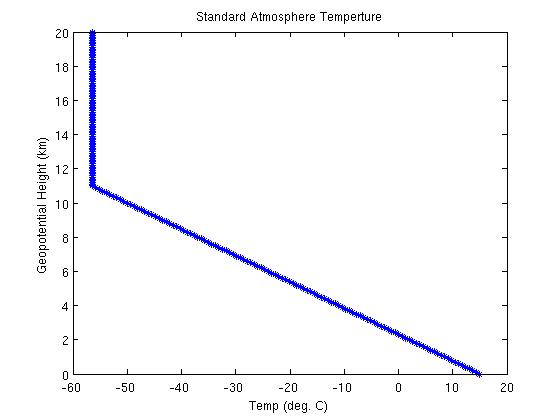
Figure 1

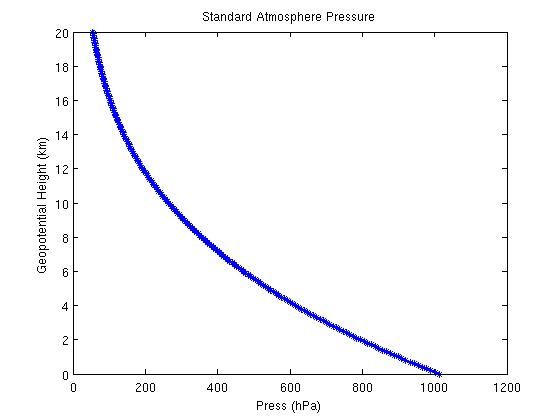
Figure 2:
Figure 2

Figure 3:
Figure 3


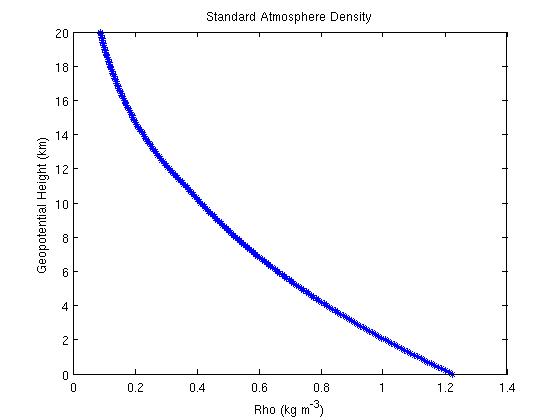
Part 2

Question 4
The fact that the semilog plots of pressure and density are not linear tells us that these quantities do not vary logarithmically with geopotential height. This means that defining a single scale height valid over the entire vertical extent of the atmosphere would not be valid, because the change in pressure or density corresponding to a decrease of 1/e of the initial geopotential height varies from one initial point to another.

Question 7
The saturated adiabatic temperature profile matched better with the profile from the U.S. Standard Atmosphere. The height at which the temperature begins to increase with height is called the tropopause, and marks the beginning of the stratosphere. This would correspond to a negative lapse rate.

Figure 4:
Figure 4

Figure 5:
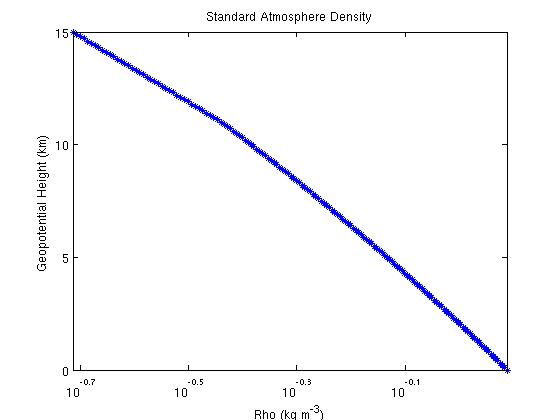
Figure 5

Figure 6:
Figure 6

Back to Main