To answer #4, we used the atmosphere function in Matlab to figure out what heights in meters correspond with the pressures given. We found that 700 hPa is about equal to a height of 3000 m and that 500 hPa is nearly equal to 5560 m. We then plugged these values in meters back into the atmosphere function to get the temperature at each level. The average temperature of these two is what we use when calculating the thickness using the hypsometric equation, which was 260.5 K.

Number 5: The hypsometric equation gave a thickness of 2562.6 m, which was very close to the estimate using the two heights found using Matlab (5560 m - 3000 m = 2560 m). This is what I expected, since the heights in meters corresponded closely with the heights I wanted in hPa using the atmosphere function.

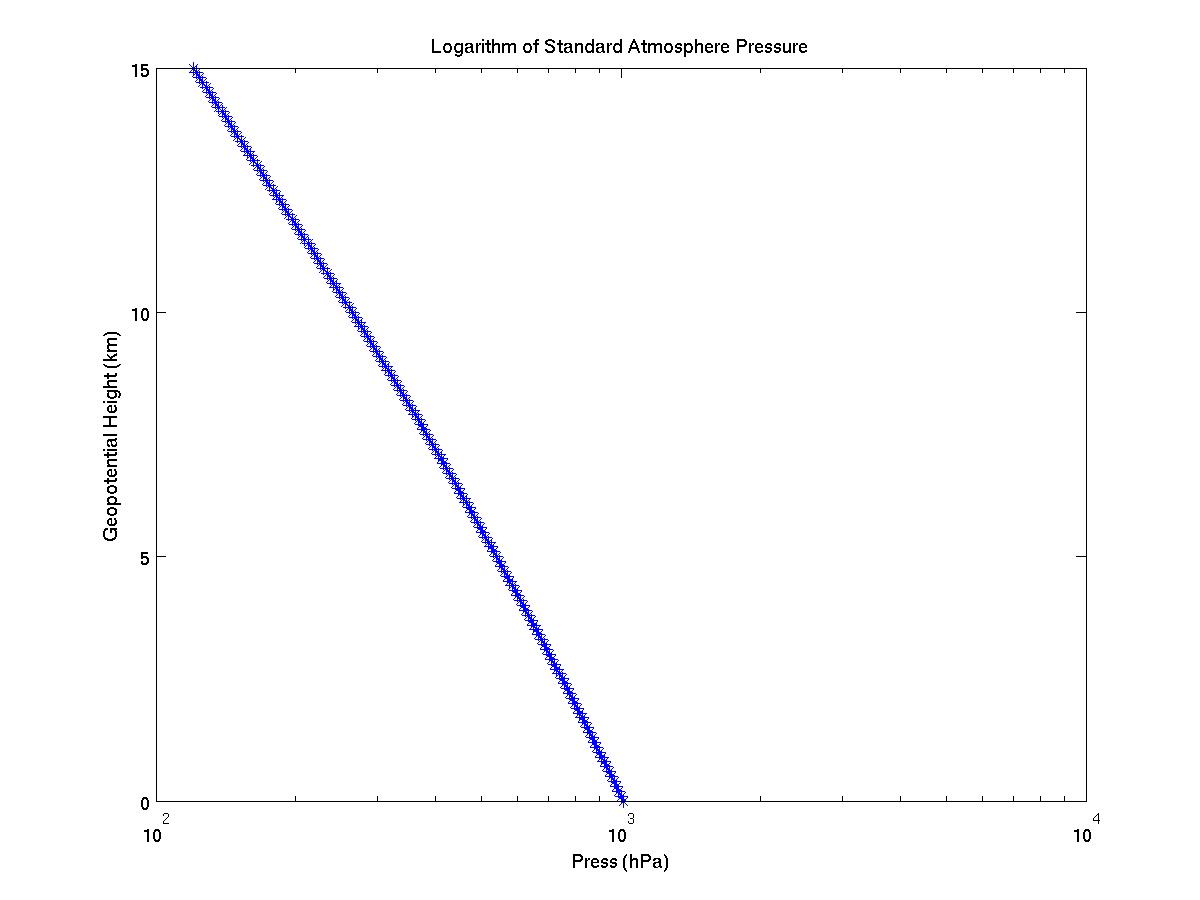
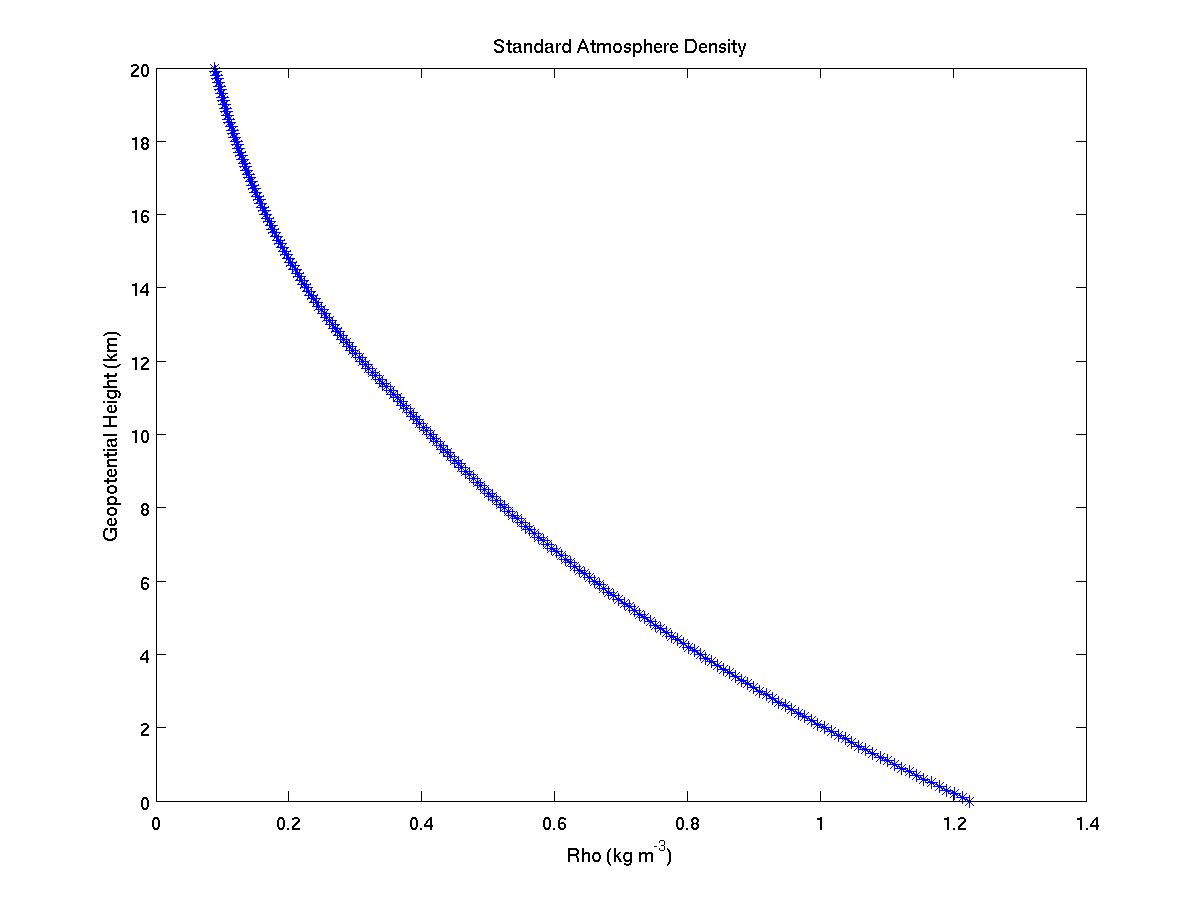
Number 4: The top two graphs in part 2 are logarithms of the original plots for pressure and density. This tells us that the rate at which the pressure changes with height differs from the rate of air density change with height. This shows that it would not make sense to define these changes with one scale height.

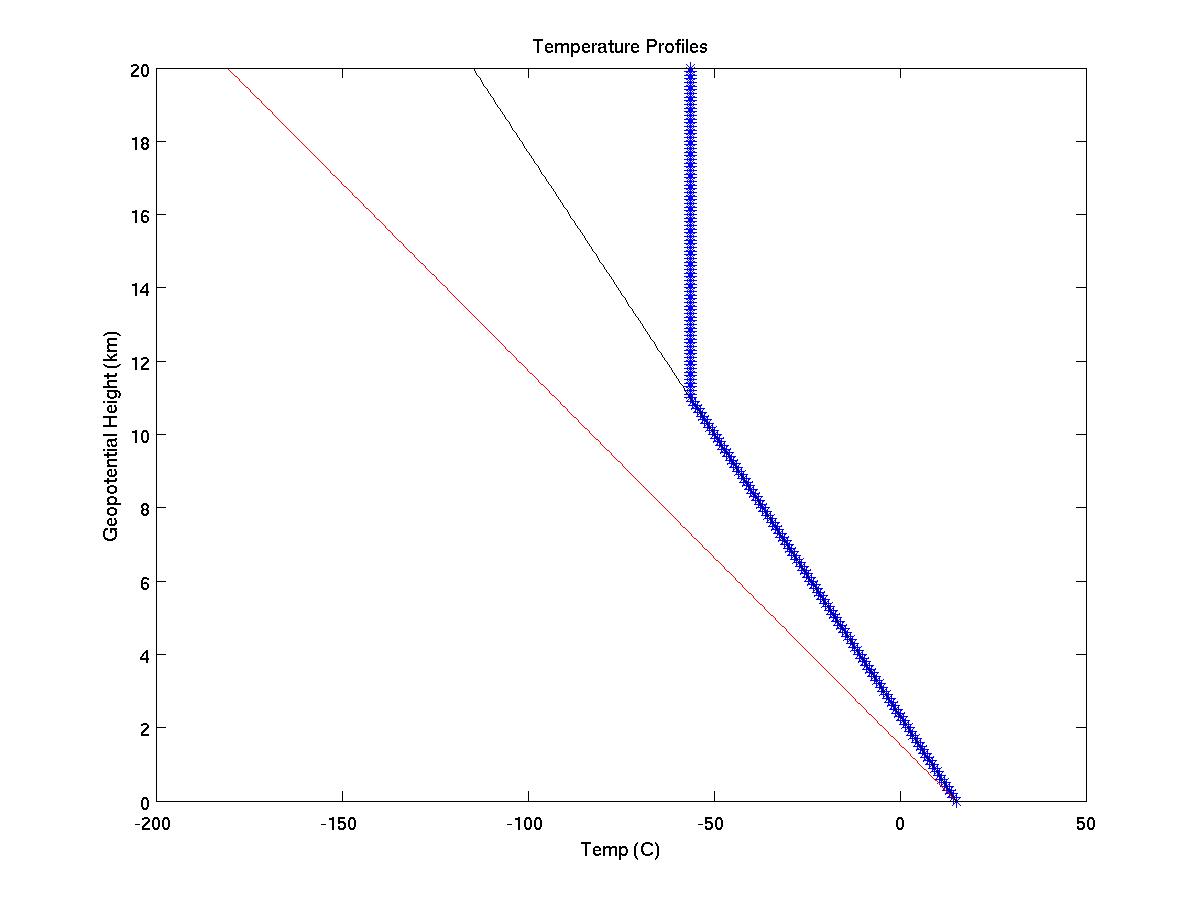
Number 7: The last graph is a plot of temperature profiles. The blue line is the standard temperature, the green line is the moist adiabatic lapse rate, and the red line is the dry adiabatic lapse rate. From this graph, you can see that the standard temperature closely resembles the moist adiabatic lapse rate until a height of 11 km, which is the tropopause. The air above the tropopause is much thinner than the air below it. Three-quarters of the total mass of the atmosphere lies in the 11 km above the surface. At the tropopause, the temperature remains constant until higher up in the atmosphere, where it begins to increase with height. When the temperature increases with height, the lapse rate is negative.