1. Introduction

The interannual variation of tropical Pacific SST known as El-Nino has a profound impact on global climate (Horel and Wallace 1981; Kang and Lau 1986; Ropelewski and Halpert 1987). The spatial pattern of the interannual SST variation has a more or less standing oscillation pattern in the central  nd eastern Pacific. Recent simulations with a coupled ocean-atmosphere GCM and intermediate models nicely reproduced the standing oscillation characteristics of SST oscillation (Zebiak and Cane 1987; Wang et al. 1995, Philander et al. 1992). However, most of simple theoretical models show a propagating mode more distinctively than the stationary component (Gill 1985; Hirst 1986, 1988; Wang and Weisberg 1994). An exception is the study by Wakata and Sarachik (1991), in which the standing oscillation of SST is reproduced by considering a more realistic basic state. Jin and Neelin (1993) investigated the propagating and stationary characters of SST in terms of different flow regimes. But, the dynamics underlined the stationary characteristics of observed SST oscillation is not fully understood yet.

The oscillatory behavior and ocean-atmosphere instability associated with ENSO are known to strongly depend on the thermodynamics determining SST anomalies in the tropics (Hirst 1986; Wakata and Sarachik 1991). Among them, the zonal advection and upwelling play the most important roles (Hirst 1986). The zonal advection excites the unstable mode propagating westward (Gill 1985), on the other hand, the upwelling mechanism produces an eastward propagating unstable mode (Philander et al. 1984), which has a speed and structure in the ocean similar to a free oceanic Kelvin wave. Hirst (1986, 1988) examined the coupled mode with both dynamics and found a slow eastward propagating unstable mode. In his model, all atmospheric and oceanic variables are strongly coupled, and thus the SST, thermocline depth, and wind anomalies are all propagating to the east with a same speed. This mode was also simulated by all sorts of numerical models (Anderson and McCreary, 1985; Neelin 1991; Lau et al. 1992). The thermocline propagation characteristics appears to be similar to the observed counterpart. But, there is little evidence of eastward propagation in observed SST variations.

The observed SST variation is very weak in the western Pacific and thus is characterized by a more or less standing oscillation confined in the central and eastern equatorial Pacific. More recently, Wakata and Sarachik (1991) simulated a SST oscillation similar to the observed using a linear version of Zebiak and Cane (1987) model. Their model is basically the same as that of Hirst (1988) but considered a more realistic ocean basic state, particularly the climatological upwelling trapped near the equator. On the basis of the results, they pointed out the importance of meridional structure of mean upwelling, to the SST oscillatory behavior. In the present study, the impact of equatorial trapped mean upwelling to the SST variation is investigated in more detail, and the SST oscillation is understood in terms of cancellation and superposition of the SST anomalies generated by oceanic Rossby and Kelvin waves.

The roles of Kelvin and Rossby waves in ENSO have been studied by many authors (Suarez and Schopf 1988; Battisti 1988, 1989; Schneider et al. 1995). Recently, ENSO is viewed as a continuing cycle whose origin is a coupled instability and whose oscillatory properties are determined by the retarded wave forcing in the presence of western boundary. The mechanism is referred to as "delayed oscillator" (Suarez and Schopf 1988; Schopf and Suarez 1988; Battisti 1988; Battisti and Hirst 1989; Schneider et al. 1995). In the delayed oscillator, the western boundary reflection of the Rossby waves excited by the wind stress associated with interannual SST anomalies produces the eastward propagating Kelvin waves, which eventually initiate a coupled instability in the eastern Pacific. Among many meridional Rossby mode, most important mode is known to be the lowest-order symmetric Rossby mode (Battisti 1988, Wakata and Sarachik 1991). In this study, to simplify the model formulation and understand the dynamics more easily, we developed a simple coupled model highly truncated with only two wave components: Kelvin wave and the gravest Rossby wave. One of the objectives of the present study is thus to examine the extent to which the highly truncated system produces a coupled unstable mode similar to that obtained with a more complicated system used by Hirst (1988) and others. Having confirmed the capability of the simple truncated model, we examine the SST oscillation mechanism and the role of wave reflections at the western and eastern boundaries in an ENSO like oscillation using the model.

Section 2 introduces the formulation of the present model with two wave components of Kelvin and lowest symmetric Rossby waves. In Section 3, the most unstable modes obtained by Hirst (1988) and Wakata and Sarachik (1991) are reproduced, and the differences between the modes are understood using the present model. The standing oscillation character of SST oscillation similar to that of Wakata and Sarachik is understood in terms of a cancellation of SST tendencies by the Kelvin and Rossby waves. Also investigated are the role of free reflected waves at the western and eastern boundaries in an ENSO like oscillation and the dependency of most unstable mode to the reflection coefficient. Summary and concluding remarks are given in Section 4.

2. Model

A simple coupled system is developed in a similar manner to that of Hirst (1988). In this paper, however, a highly truncated system with only two wave components, the Kelvin wave and the gravest symmetric Rossby wave, is developed to simplify the system. The simplification is based on the previous studies (e.g., Battisti 1989), which pointed out that the ENSO wave dynamics is governed mostly by the two wave components.

As in Hirst (1988), a linear shallow water equation is used for the ocean model with a long wave approximation in an equatorial b plane, and the thermodynamic equation for SST has the linearized zonal advection and upwelling terms. After introducing a wave solution in time (e^-iwt ), the nondimensional equations can be written as

where h is the thermocline depth, u and v the zonal and meridional currents of upper ocean, respectively, and T the SST. w is the frequency, and k and d are the Rayleigh friction and Newtonian cooling coefficients, respectively. The variables are the nondimensional quantities with respect to a length scale of (c_o/b)^1/2=3.6x10⁵m and a time scale of (c_ob)^-1/2 = 1.2 x 10⁵ s. In the SST equation of Eq. (4), T_x is the background zonal SST gradient, K_T the entrainment thermal coefficient. t is the wind stress. In the present study, the wind stress is simply parameterized in terms of SST. This kind of parameterization was used by Wang and Weisberg (1994) and Wang and Fang (1996). In particular, Wang and Weisberg determined the wind stress as t=mT(x+q) , where m is the wind stress coupling coefficient and q(=0.3p) the phase difference between the surface wind and SST. The phase difference is indicated by several authors such as Hoskins and Karoly (1981) and Rasmusson and Carpenter (1982). We thus adapt the Wang and Weisberg's parameterization.

Now as in Gill (1980) and Hirst (1988), new variables s = h+u and r = h-u are introduced in Eqs. (1) - (4), and then s, r, T are expressed as sums of symmetric Hermit functions, e.g.,

and v as a sum of antisymmetric Hermit functions. Upon using the recurrence formula of Hermit functions and the orthogonal relationship between the functions, the v_n and r_n can be eliminated. Then Eqs. (1) - (4) can be expressed in terms of s_n and T_n . Details of the procedure mentioned above can be found in Hirst (1988). Now truncating the system with only two waves components of the Kelvin wave (n=0) and the lowest symmetric Rossby wave (n=2), we can obtain the following set of equations.

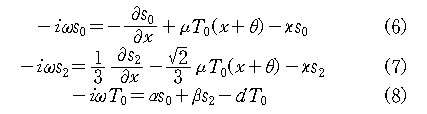
where and . For K_T constant in the domain, that Hirst (1986, 1988) used, and . On the other hand, Wakata and Sarachik (1991) used K_T as a function of y by considering a climatological mean upwelling distribution confining near the equator. In this study, we will consider both cases for K_T. The values of the coefficients used in the present study are summarized in Table 1.

For an unbounded ocean case, the x-dependence can be expanded in terms of sinusoidal wave solutions (e^ikx ). Then, the equations of (6)-(8) provided three kinds of wave mode. Without the damping k=0 and wind forcing m=0, Eqs. (6) and (7) provide the dispersion relationships for a free Kelvin wave (w = k) and a free Rossby wave (w = -k/3) for a zonal wavenumber k. When the wind forcing and damping introduced, the Kelvin and Rossby waves become damping modes and a coupled mode is generated. The behavior of the coupled mode depend on the values of a and b. With a choice of the values used by Hirst (1986), the coupled mode is unstable and moves to the east with a slow wave speed for long waves. The coupled mode with a short zonal scale is damping. It is noted that the wave solutions of the present model (not shown) are very similar to those obtained by Hirst (1986), indicating that the unstable coupled mode is reasonably well represented by the two wave component model.

For a bounded ocean, the finite difference method is applied to x-dependence of the variables in Eqs. (6)-(8). The spatial scale of the ocean basin chosen is 16200 km and the ocean basin is divided by the equally spaced 100 grids. The boundary conditions at the western and eastern boundaries used are the same as those of Hirst (1988). Thus, s₀(x_W)=(2^1/2/2)s₂(x_W) and s₂(x_E)=(2^1/2/2)s₀(x_E), where x_W and x_E are the western and eastern boundaries, respectively. The eigenmodes of Eqs. (6)-(8) are obtained in the grid system, and the most unstable modes are discussed in the next section.

3. Results

The most unstable modes in a closed ocean basin obtained by Hirst (1988) and Wakata and Sarachik (1991) are reproduced using the present two wave component model. As noted in the previous section, the main difference between the two studies is due to different meridional distributions of the upwelling coefficient K_T and thus the different values of a and b. Two sets of a and b are computed using the values of T_x and K_T used by Hirst (1988) and Wakata and Sarachik (1991). a and b are in a nondimensional unit, respectively, 1.65x10^-3 and 0.64x10^-3 for the Hirst case and 1.0x10^-3 and -0.52x10^-3 for the Wakata and Sarachik case. For convenience, the model using Hirst's values is referred to as Model A, and the model using Wakata and Sarachik's values as Model B.

Time variations of the most unstable mode of Model A are shown in Fig. 1 for thermocline depth and SST. In this paper, the time variation of the spatial structure of unstable mode will be examined by the real part and e-folding time of the mode. The e-folding time scale of the unstable mode shown in Fig. 1 is about two years. Consistent with the Hirst model, both height and SST are propagating to the east with a same speed. On the other hand, the unstable mode of Model B shown in Fig. 2 is characterized more or less by a standing oscillation. In particularly, SST variations are confined in the central and eastern Pacific, and those in the western Pacific are very weak although the thermocline variations are relatively large. Also noted that in addition to the dominant standing oscillation, some eastward propagation signal is also seen in the thermocline variation. Both Model A and B results are very similar to those of Hirst (1988) and Wakata and Sarachik (1991), respectively, indicating that the essential structure of the coupled unstable mode is determined by the two wave components.

Fig. 1. Phase-longitude cross section of the real part of most unstable mode along the equator. (a) and (b) are thermocline depth and SST obtained with a constant upwelling coefficient over the model domain, respectively. Here 360o in y axes corresponds to one period, and time processes in the direction of increasing phase angle.

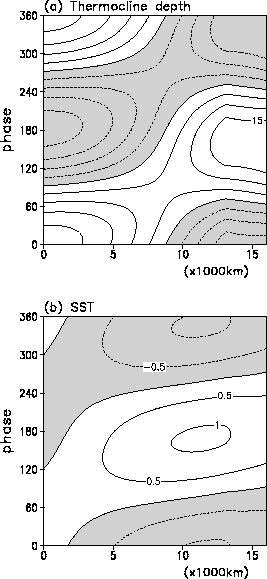
Fig. 2. As in Fig. 1 except for the case of the meridional distribution of upwelling coefficient confined near the equator.

The difference between the two model results can be interpreted using Eq. (8), which can be expressed as

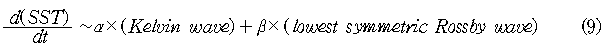
For the Hirst (Model A) case, both a and b are positive values and a is much bigger than b. Therefore, SST tendency is mainly controlled by the Kelvin wave of thermocline depth which propagates to the east. On the other hand, for the case of Model B, a and b have different signs. Therefore, Kelvin and Rossby contributions cancels each other over the region where both waves have a same sign. Since the spatial and temporal variations shown in Fig. 2 are similar to those of observed ENSO, we will focus on the unstable mode of Model B in the rest of this paper. It is noted that Model B contains a single unstable mode, which is shown in Fig. 2, and the other modes all damped in time. The e-folding time of the unstable mode is about two years.

Fig. 3 shows a half cycle of variations of SST, Kelvin and lowest symmetric Rossby waves of the unstable mode produced by Model B. The variations are plotted with a 30 degree phase interval. As seen in the previous figure, large SST variations are confined in the central and eastern equatorial Pacific, and the variations are mainly characterized by a standing oscillation. But some eastward propagation is also seen in the central part of the domain. The eastward propagation is more clear in the variations of Kelvin part of thermocline depth. When the signal arrives in the eastern Pacific, it becomes amplified (Figs. 3j-3l). On the other hand, the Rossby part of thermocline depth is characterized by a standing oscillation which has large amplitude in the western Pacific. The Rossby wave is excited mainly by the wind stress associated with SST. The variations shown in Fig. 3 can be interpreted in terms of the delayed oscillator mechanism, as discussed by Wakata and Sarachik (1991). The SST and thus wind stress excite Rossby wave in the western Pacific, which in turn provides Kelvin wave signal over the western Pacific by the boundary reflection (Figs. 3a, 3g, and 3m). The Kelvin wave signal propagates to the east and reduces the thermocline depth anomalies pre-existing in the central and eastern Pacific, which have a sign negative to that propagated from the west (Figs. 3a-3c, 3g-3i, and 3m-3o). The Kelvin wave signal eventually changes the sign of thermocline depth and SST over the central and eastern Pacific (Figs. 3d and 3j), and thereafter a negative phase becomes amplified there by a coupled instability (Battisti 1988). The next phase of the oscillation operates as mentioned above except with a reversed sign (Figs. 3f, 3l, and 3r). It is also noted that there exists the reflection from Kelvin to Rossby waves in the eastern boundary. But, since the Rossby waves forced by SST dominate in the western and central Pacific, the reflected Rossby wave signal appears not much to affect the wave amplitudes to the west.

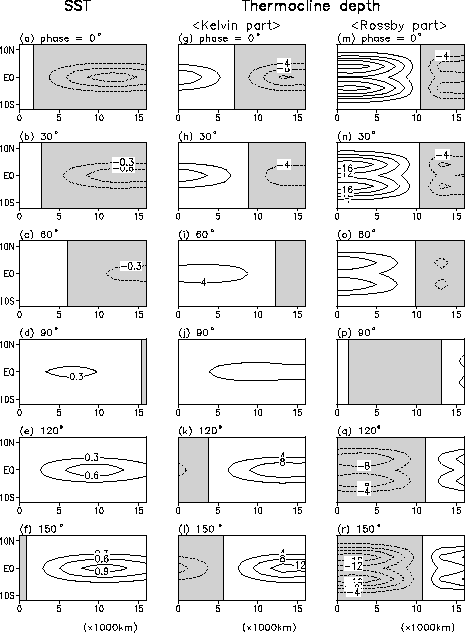
Fig. 3. Time evolution of the real part of unstable mode obtained with the model B. The thermocline depths associated with Kelvin and Rossby waves and SST are plotted with a phase interval of 30 degree. The units of depth and SST are meter and oC, respectively.

Overall, the variations of SST and gravest Rossby wave are characterized by standing oscillations. On the other hand, the Kelvin wave has a propagation component, which is generated by the reflection of the Rossby wave. This Kelvin wave propagation has a negative feedback to the forced waves in the eastern Pacific and thus plays as a transition mechanism of the oscillation. It is also noted that the Rossby wave generated by the eastern boundary reflection has an opposite sign to that of the forced Rossby wave in the western Pacific. Thus, the most important characteristics of the model are the standing oscillation of SST (wind forcing) and the wave reflections at the boundaries, particularly the eastward propagation of Kelvin wave reflected at the western boundary. We investigate the SST variation and the role of wave reflections in the oscillation separately in below.

The SST variations expressed by Eq. (9) are due to the Kelvin and Rossby waves. Each wave contribution to SST tendency of Model B along the equator is computed and plotted in Fig. 4 for one oscillation cycle. The SST tendency induced by Kelvin wave shown in Fig. 4a has relatively large eastward propagation component, although large amplitudes appear in the western and eastern Pacific. On the other hand, the Rossby wave contribution (Fig. 4b) is characterized by more or less a standing oscillation with a large amplitude in the western Pacific. The westward propagation in the eastern Pacific is related to the Rossby waves reflected at the eastern boundary. Very interestingly, there is a cancellation between the Kelvin and Rossby wave contributions in the western and eastern Pacific. In particular, almost complete cancellation happens in the western Pacific. This cancellation can be understood using Eq. (9). As noted previously, a and b in Eq. (9) have different signs and the absolute magnitude of a is almost twice that of b. As shown in Fig. 3, the Kelvin wave in the western Pacific has a same sign as that of Rossby wave, but its amplitude is half of Rossby wave amplitude. Thus the SST variation in the western Pacific should be very weak by almost complete cancellation of the two wave contributions. In the eastern Pacific, on the other hand, the Kelvin wave amplitude is bigger than that of Rossby wave. Thus, the Rossby wave contribution is a minor part in the SST tendency in the eastern Pacific. In summary, the weak SST variation in the western Pacific and thus the standing oscillation character of basin-scale SST are mainly due to the cancellation of SST tendencies induced by Kelvin and Rossby waves.

Fig. 4. (a) Phase-longitude cross section of the SST tendency along the equator induced by the Kelvin wave. (b) As in (a) except by the lowest symmetric Rossby wave. Unit is oC/month.

We now examine the transition mechanism of the oscillation, which is the wave reflections at the boundaries. To examine the forced and reflected wave activities along the equator, the zonal means of the thermocline depths associated with forced and reflected free waves are obtained and plotted in Fig. 5. The reflected free wave components are computed based on the following wave equations with a damping.

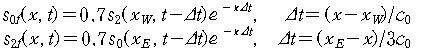
where s_0f and s_2f are the reflected free Kelvin and Rossby waves, respectively. x_W and x_E are the western and eastern boundaries, respectively, c_o is the Kelvin wave speed of 2.9 ms^-1, and k the damping coefficient. The above equations are formulated based on the fact that the reflection coefficient at both boundaries used in the present model is 0.7 and the reflected waves propagate with free wave speeds. The forced wave component is obtained by subtracting the free wave components from the total.

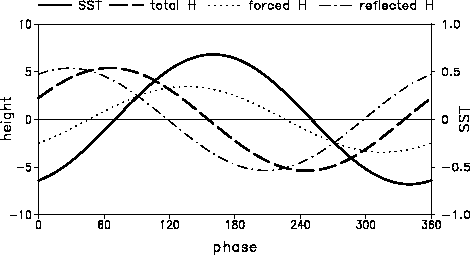
Fig. 5. Time changes of the zonal means along the equator for one cycle. Solid, dashed, dotted, and dot-dashed lines indicate SST, thermocline depth, the forced and reflected parts of thermocline depth, respectively.

As shown in the figure, the zonal mean depth associated with reflected free waves has a large phase lag with the zonal mean SST. The minimum (largest negative) value of the zonal mean depth appears about 40 degree phase after the maximum SST. On the other hand, the zonal mean depth associated with forced wave components has little phase difference with the zonal mean SST. It is very interesting that the amplitude of zonal-mean depth associated with the reflected waves has slightly larger amplitude than that of forced waves. This is because the forced waves have large amplitudes in the Rossby component and the reflected Kelvin wave spreads along the equator with a relatively fast free wave speed. By the cancellation between the forced and reflected free waves, the zonal-means of thermocline depth and SST have a phase lag of about 90 degree. Thus, the ocean memory indicated by the thermocline depth leads the SST and wind forcing by a quadrature cycle. The time lag between the zonal mean thermocline and SST produces the oscillation of ENSO like system (Schneider et al. 1995; Jin 1997).

As shown above, the wave reflection at the boundaries play a critical role for the oscillation. Now a question can arise for the reflection coefficients at both western and eastern boundaries. In the present model so far, both coefficients used are set to be a theoretical value of 0.7. But, in reality, the boundaries have complex geometrical shapes and in particular, the Kelvin wave in the western boundary is resulted from superposition of reflections of many Rossby modes (Chao and Philander 1993). Thus, it is difficult to determine the reflection coefficients, if the reality is considered. With this reason, we examine the dependency of the oscillation frequency and growth rate of the unstable mode of the present system on the reflection coefficients at the western and eastern boundaries.

In Fig. 6a, the frequency and growth rate are plotted for different values of reflection coefficient at the western boundary. In this case, the coefficient at the eastern boundary is fixed with a value of 0.7. The figure indicates that no oscillation occurs for the coefficients less than 0.54. A very low-frequency oscillation starts at the coefficient of 0.54 with a minimum growth rate. As the coefficient increases from 0.54 to one, both oscillation frequency and growth rate becomes increased. The critical value of the coefficient 0.54 for starting the oscillation indicates that a sufficient negative feedback by the reflection is a necessary condition for the oscillation. It is understandable that the growth rate decreases as the coefficient increases from 0 to 0.54. But what is a interesting point here is that the growth rate increases as the coefficient increases from the critical value of 0.54. This is related to the decrease of oscillation period, because the accumulation of negative feedback by the reflection decreases as the period of oscillation decreases. Fig. 6b is for the case of different values of eastern boundary but with a fixed coefficient 0.7 at the western boundary. The figure indicates that the growth rate does not much depend on the reflection coefficient at the eastern boundary, but the coefficient appears to affect the oscillation period. It is interesting to note that low values of the reflection coefficient is more favorable to a low-frequency oscillation.

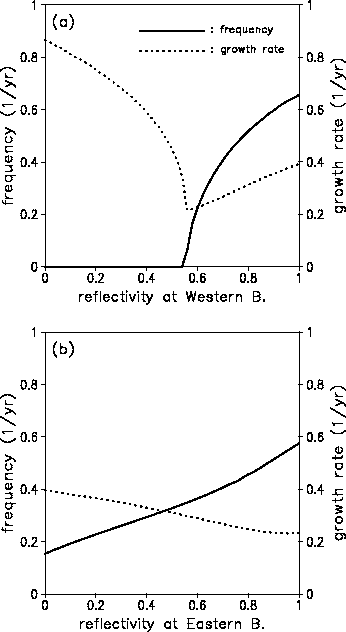
Fig. 6. (a) Period and growth rate of the unstable mode as a function of reflection coefficient at the western boundary. The reflection coefficient at the eastern boundary is set to 0.7. (b) As in (a) except as a function of reflection coefficient at the eastern boundary and the coefficient at the western boundary set to 0.7. Solid and dotted lines indicate frequency and growth rate, respectively.

Fig. 6 indicates that the oscillation character of the present model is sensitive to western boundary reflection, and the eastern boundary reflection modifies the oscillation period. Now an interesting question immediately raised is a realistic regime of the western boundary reflection. Two factors should be considered in reality, which are the open channel in the western Pacific, particularly Indonesian throughflow, and the superposition of many meridional Rossby waves. The throughflow effect will certainly reduce the reflection coefficient, and Battisti (1989) indicates that the interference of many meridional Rossby waves also reduces the coefficient. A realistic reflection coefficient at the western boundary is hardly determined by observations, but its value appears to be smaller than the theoretical value of 0.7.

4. Summary and concluding remarks

A simple model of ENSO like oscillation is developed using the two wave components: Kelvin wave and lowest symmetric Rossby wave. The oscillation is best described by the forced waves associated with a standing oscillation of SST and the reflected free waves generated at the western and eastern boundaries. The standing oscillation character of basin-scale SST in the central and eastern Pacific and the weak SST variation in the western Pacific are explained by cancellation of SST tendencies induced by Kelvin and Rossby waves. The reflected waves play a negative feedback mechanism to the oscillation system. The oscillation period and instability depend on the reflectivity of western and eastern boundaries.

The contributions of wave components to SST tendency can be explained as follows. In the presence of zonal temperature gradient of basic state, a positive Kelvin wave produces positive SST tendency by zonal advection, but a positive Rossby wave produces a negative tendency. In the presence of background upwelling, the positive depth associated with both waves produces a positive tendency of SST by upwelling effect. Therefore, Kelvin wave contribution to SST tendency is reinforced by both effects. For the Rossby wave, on the other hand, the temperature advection and upwelling effects have different signs from each other. For the basic states used by Hirst (1988) and others, the upwelling effect is bigger than that of zonal temperature advection. In this case, the Kelvin and Rossby wave contributions to SST tendency has a same sign. However, For the equatorially trapped upwelling (Wakata and Sarachik 1991 and the present study), the narrow upwelling has to change a broad scale SST, and therefore its effect is less than that of zonal advection. In fact, the meridional scale of upwelling coefficient is much smaller than that of SST in the present model. In this case, the Kelvin and Rossby wave contributions have different signs from each other. For a realistic parameter range, the absolute value of the coefficient for Kelvin wave contribution, a in Eqs. (8) and (9), is about twice bigger than that of the coefficient for the Rossby wave contribution. In the western Pacific, the amplitude of Kelvin wave is about half of the Rossby wave, since the Kelvin waves are produced mainly by the reflection of Rossby waves. As a result, the SST induced by Kelvin wave is almost completely canceled by the Rossby wave contribution in the western Pacific. However, in the eastern Pacific, Kelvin wave contributes a major part of wave amplitude. In this region, therefore, SST is mainly determined by the Kelvin wave activity and Rossby wave contribution plays a minor role in the SST variation.

The Rossby waves indirectly affect the SST in the eastern Pacific by generating Kelvin waves at the western boundary. The reflected Kelvin wave plays a negative feedback mechanism to the oscillation. The zonal mean depth associated with reflected free waves is almost out of phase with the SST, whereas the zonal mean associated with forced wave component is almost in phase of the SST. By a large cancellation between the zonal means of forced and free waves, the zonal means of thermocline depth and SST have a phase lag of about 90 degree. The quadrature phase lead of ocean memory (thermocline depth) to the SST produces an ENSO like oscillation. Several studies already indicated that the zonal mean thermocline depth plays as a ocean memory of ENSO (Zebiak and Cane 1987; Schneider et al. 1995; Jin 1997). But in order to understand the oscillation mechanisms in more detail, a separate examination of zonal mean and deviation may be needed by using the model containing both components separated. This study will be a next subject of our work.

Acknowledgments

The authors appreciate Profs. Bin Wang and Fei-Fei Jin for helpful discussions about this work during the first author's visit to the University of Hawaii for January and February of 1997. We also appreciate Prof. T. Yamagata for his continuous interest in our work. This work is supported by the Basic Science Research Program of the Ministry of Education in Korea, BSRI-96-5410, and partically by the Korea Meteorological Research Institute.

References

Anderson, D. L. T., and J. P. McCreary, 1985: Slowly propagating disturbances in a coupled ocean-atmosphere model. J. Atmos. Sci., 42, 615-629.

Battisti, D.S., 1988: Dynamics and thermodynamics of a warming event in a coupled tropical atmosphere-ocean model. J. Atmos. Sci., 45, 2889-2919.

____, and A.C. Hirst, 1989: Interannual variability in a tropical atmosphere-ocean model: Influence of the basic state, ocean geometry and nonlinearity. J. Atmos. Sci., 46, 1687-1712.

____, 1989: On the role of off-equatorial ocean Rossby waves during El-Nino. J. Phys. Oceanogr., 19, 551-559.

Chao, Y. and S.G.H. Philander, 1993: On the structure of the Southern Oscillation. J. Climate, 6, 450-469.

Gill, A.E., 1980: Some simple solutions for heat-induced tropical circulation. Quart. J. Roy. Meteor. Soc., 106, 447-462.

____, 1985: Elements of coupled ocean-atmosphere models for the tropics. Coupled Ocean-Atmosphere Models. J. C. J. Nihoul, Ed., Elsevier Oceanography Series, 40, Elsevier, 303-327.

Hirst, A.C., 1986: Unstable and damped equatorial models in simple coupled ocean-atmosphere models. J. Atmos. Sci., 43, 606-630.

____, 1988: Slow instabilities in tropical ocean basin-global atmosphere models. J. Atmos. Sci., 45, 830-852.

Horel, J., and J.M. Wallace, 1981: Planetary scale atmospheric phenomena associated with the Southern Oscillation. Mon. Wea. Rev., 109, 813-829.

Hoskins, B.J., and D.J. Karoly, 1981: The steady linear response on a spherical atmosphere to thermal and orographic forcing. J. Atmos. Sci., 38, 1179-1196.

Jin, F.-F., 1997: An equatorial ocean recharge paradigm for ENSO. Part I: Conceptual model. Submitted to J. Atmos. Sci.

____, and J.D. Neelin, 1993: Modes of interannual tropical ocean-atmosphere interaction - a unified view. Part I: Numerical results. J. Atmos. Sci., 50, 3477-3503.

Kang, I.-S., and N.-C. Lau, 1986: Principal modes of atmospheric variability in model atmosphere with and without anomalous sea surface temperature forcing in the tropical Pacific. J. Atmos. Sci., 43, 2719-2735.

Lau, N.-C., S. G. Philander, and M. J. Nath, 1992: Simulation of ENSO-like phenomena with low-resolution coupled GCM of the Global ocean and atmosphere. J. Climate, 5, 284-307.

Neelin, J.D., 1991: The slow sea surface temperature mode and the fast-wave limit: analytic theory for tropical interannual oscillation and experiments in a hybrid coupled model. J. Atmos. Sci., 48, 584-606.

Philander, S. G. H., T. Yamagata and R. C. Pacanowski, 1984: Unstable air-sea interactions in the tropics. J. Atmos. Sci., 41, 604-613.

____, R. C. Pacanowski, N.-C. Lau, and M. J. Nath, 1992: Simulation of ENSO with a global atmospheric GCM coupled to a high-resolution tropical Pacific ocean GCM. J. Climate, 5, 308-329.

Rasmusson, E.M. and T.H. Carpenter, 1982: Variations in tropical sea surface temperature and surface wind fields associated with the Southern Oscillation/El Nino. Mon. Wea. Rev., 110, 354-384.

Ropelewski, C.F., and M.S. Halpert 1987: Global and regional scale precipitation patterns associated with the El Nino/Southern Oscillation. Mon. Wea. Rev., 115, 1606-1626.

Schneider, E.K., B. Huang, and J. Shukla, 1995: Ocean wave dynamics and El Nino. J. Climate, 8, 2415-2439.

Schopf, P.S. and M.J. Suarez, 1988: Vacillations in a coupled atmosphere-ocean model. J. Atmos. Sci., 45, 549-566.

Suarez, M.J. and P.S. Schopf, 1988: A delayed oscillator for ENSO. J. Atmos. Sci., 45, 3283-3287.

Wakata, Y., and E.S. Sarachik, 1991: Unstable coupled atmosphere-ocean basin modes in the presence of a spatially varying basic state. J. Atmos. Sci., 48, 2060-2077.

Wang, B., T. Li, and P. Chang, 1995: An intermediate model of the tropical Pacific ocean. J. Phys. Oceanogr., 25, 1599-1616.

____, Z. Fang, 1996: Chaotic oscillations of tropical climate: A dynamic system theory for ENSO. J. Atmos. Sci., 53, 2786-2802.

Wang, C., and R.H. Weisberg, 1994: On the "slow mode" mechanism in ENSO-related coupled ocean-atmosphere models. J. Climate, 7, 1657-1667.

Zebiak, S.E., and M.A. Cane, 1987: A model El-Nino-Southern Oscillation. Mon. Wea. Rev., 115, 2262-2278.