SINGLE-DOPPLER VELOCITY RETRIEVAL AND RADAR DATA ASSIMILATION AT THE CENTER FOR ANALYSIS AND PREDICTION OF STORMS (CAPS)

Alan Shapiro^*

Center for Analysis and Prediction of Storms (CAPS)/School of Meteorology
University of Oklahoma, Norman, Oklahoma USA

The Center for Analysis and Prediction of Storms (CAPS) was established at the University of Oklahoma in 1988 as one of the National Science Foundation's first 11 Science and Technology Centers. Its formal mission is to demonstrate the practicability of storm-scale numerical weather prediction and to develop, test and validate a regional forecast system appropriate for operational, commercial, and research applications.

The principal scientific research and development efforts in CAPS can be broken into three broad categories: (i) Model Development, (ii) Data Analysis (Aquisition and Control), and (iii) Data assimilation and Prediction Studies. The model development program involves the construction and operational testing of a nonhydrostatic prediction model known as the Advanced Regional Prediction System (ARPS) (Droegemeier et al. 1996, Xue et al. 1996a,b). The heart of the data analysis program is the ARPS Data Analysis System (ADAS) (Brewster 1996), a package which can incorporate conventional observational data (e.g., surface, mesonet, rawinsonde) as well as data from Doppler radars and radar-derived data. The data assimilation effort has placed a special emphasis on the use of single-Doppler radar data. At CAPS, the single-Doppler activities have been proceeding along several fronts: full model adjoint techniques, forward-assimilation methods, and simple single-Doppler velocity retrieval (SDVR) techniques that seek to determine the complete wind vector field given only single-Doppler radar data.

This article will consider, in turn, the latter two approaches: SDVR and forward radar data assimilation. Taken together, these techniques have important implications for hazard warning, nowcasting, guidance for aviation operations, as well as for the initialization of numerical weather prediction models.

Early work on single-Doppler velocity retrievals (SDVR) focused on velocity azimuth display (VAD) and volume velocity processing (VVP) methods of analysis, whereby radial velocity measurements were fit to simple (e.g., linear) wind models (e.g., Lhermitte and Atlas 1961; Browning and Wexler 1968; Waldteufel and Corbin 1979; Koscielny et al. 1982).

Techniques to estimate the velocity field in terms of the objectively determined motion of radar echo patterns have also received much attention (e.g., Zawadzki 1973; Rinehart 1979; Tuttle and Foote 1990). These techniques have been applied to both conventional and Doppler radar data. Echo motion in these studies is usually obtained by tracking echo centroids or following cross-correlation maxima of features appearing in consecutive radar scans.

More recently, single-Doppler retrieval/assimilation schemes have exploited the full equations of motion, using either a forward assimilation scheme (Liou et al. 1991) or an adjoint formulation. For example, the numerical model adjoint retrievals of Sun et al. (1991), Sun and Crook (1994), and Kapitza (1991) use methods of optimal control theory to adjust the initial state variables to minimize the discrepancies between the observed variables and the model-predicted variables.

SDVR algorithms based on ``simple adjoint formulations'' are also being investigated (e.g., Qiu and Xu 1992; Xu et al. 1994a,b, 1995; Laroche and Zawadzki 1994, 1995). These techniques apply four-dimensional variational methods to simple systems (e.g., reflectivity and/or radial velocity conservation principles or subsets of the full equations of motion), rather than the complete equation set of a numerical model. As an example of this type of technique, we will examine (in section 4) a new hybrid wind retrieval technique similar to the Xu et al. and Laroche and Zawadzki approaches.

Other (non-adjoint) techniques based on the reflectivity conservation equation include the least squares formulation of Zhang and Gal-Chen (1996) and a ``two-scalar'' algorithm (Shapiro et al. 1995a, Weygandt et al. 1995). As an example of this simple type of retrieval, we will examine the Shapiro et al. (1995a) technique in the next section.

The analysis is performed in a left-handed spherical polar $(r, \phi, \theta)$ coordinate system. We specify the local vertical through the radar at ${\theta}={\pi}/2$ and the northerly azimuth angle at ${\phi}$ =0. The (known) radial velocity component is denoted by v_r, and the (unknown) polar and azimuthal velocity components are denoted by $v_{\theta}$ and $v_{\phi}$ respectively. We assume that the (logarithm) radar reflectivity, R, satisfies a conservation equation of the form,

$\begin{displaymath} {\frac{{\partial}R}{{\partial}t}} + v_{r}{\frac{{\partial}R}... ...eta}}}~=~w_{t}{\frac{{\partial}R}{{\partial}z}},~~~~~~~~~~(3.1)\end{displaymath}$

$\begin{displaymath} \frac{1}{r^{2}}\frac{\partial (r^{2}v_{r})}{\partial r} + {\... ...}{r{\cos}{\theta}}}\frac{\partial v_{\phi}}{\partial \phi}~=~0.\end{displaymath}$

$\begin{displaymath} v_{\phi}~=~{\frac{{\partial}Q}{{\partial \theta}}},~~~~~v_{\... ...{0}}^{\theta} \cos {\theta}^{\prime}v_{r}d{{\theta}^{\prime}}),\end{displaymath}$

$\begin{displaymath} {\frac{{\partial}Q}{{\partial \theta}}}{\frac{{\partial}R}{{... ...ac{{\partial}R}{{\partial \theta}}} + K_{A}~=~0,~~~~~~~~~~(3.2)\end{displaymath}$

$\begin{displaymath} \frac{D{\vec{v}}}{Dt}~=~{\frac{{\partial}{\vec{v}}}{{\partia... ... V{\frac{{\partial}{\vec{v}}}{{\partial}y}}~=~0.~~~~~~~~~~(3.3)\end{displaymath}$

Applying the D/Dt operator to the reflectivity conservation equation, and making use of (3.3), we obtain a conservation equation for $B~\equiv~DR/Dt$ . This second scalar conservation equation can be written as,

$\begin{displaymath} {\frac{{\partial}Q}{{\partial \theta}}}{\frac{{\partial}B}{{... ...ac{{\partial}B}{{\partial \theta}}} + K_{B} = 0,~~~~~~~~~~(3.4)\end{displaymath}$

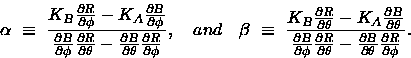
$\begin{displaymath} \alpha~\equiv~\frac{K_{B}{\frac{{\partial}R}{{\partial \phi}... ...l}B}{{\partial \theta}}}{\frac{{\partial}R}{{\partial \phi}}}}.\end{displaymath}$

$\begin{displaymath} \frac{{\partial^{2}}Q}{{\partial}{{\phi}^{2}}} + \frac{{\par... ...+ {\frac{{\partial}{\beta}}{{\partial \theta}}},~~~~~~~~~~(3.5)\end{displaymath}$

Unfortunately, this two-scalar (R and B) retrieval is faced with a singularity problem analogous to the one faced by the one-scalar scheme. In the present case the difficulty arises when the denominators of $\alpha$ and $\beta$ vanish. This can happen if the gradients of either (or both) of the two scalars vanishes or if the two scalars are (locally) functionally dependent on each other so that there is, in effect, only one conserved scalar. We thus found it desirable to reject $\alpha$ and $\beta$ in regions where the estimated error in the denominator exceeded the magnitude of the denominator. Characteristic errors of 0.1 dBZ for R and 0.1 dBZ/(time step) for B were used to derive this estimate.

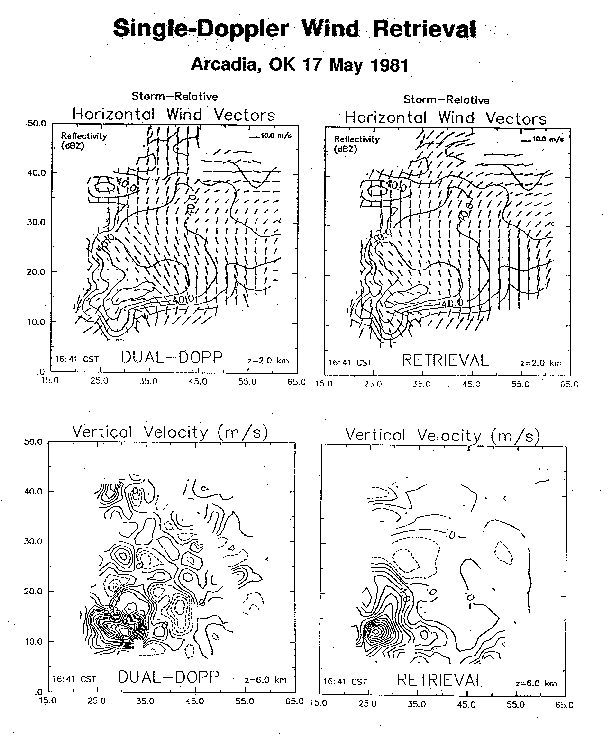$\begin{figure} \par \centerline{ \psfig {file=Fig1.ps,height=7.5in} } \par\end{figure}$

Fig. 1. (left) Dual-Doppler derived and (right) retrieved horizontal wind vectors and vertical velocity at z = 2 km for a supercell thunderstorm dataset (Arcadia, OK, 17 May 1981). Vectors are plotted in storm-relative reference frame. Reflectivity from Cimarron (input) radar contoured at 10 dBz intervals. Origin of coordinate system (0,0) coincides with location of Cimarron radar, southwest of storm. [From Weygandt et al. 1995]

We also assigned thresholds to the magnitudes of $\alpha$ and $\beta$ beyond which they were rejected. Since $\alpha$ and $\beta$ are (approximately) linearly related to $v_{\theta}$ and $v_{\phi}$ , rejection thresholds for $\alpha$ and $\beta$ could be cast, approximately, in terms of thresholds on $v_{\theta}$ and $v_{\phi}$ .

In addition, we found that in cases of strong mean wind, the retrieval could be greatly improved by working in a moving reference frame (Weygandt et al. 1995). The optimum reference frame motion was determined by the mean wind (as estimated by single-Doppler wind data) rather than by the reflectivity-pattern translation components.

An example of single-Doppler retrieved winds obtained with radar data from a heavy rain case (a supercell thunderstorm) is presented in Fig. 1. Also shown are retrieval results from an Oklahoma squall line (Fig. 5, to be compared with dual-Doppler winds in Fig. 3). In both cases a good agreement is found between the single-Doppler retrieved winds and the corresponding dual-Doppler analyzed winds.

The new retrieval described herein estimates the horizontal wind field at low altitudes (small polar angles) using a simple four-dimensional variational (4DVAR) approach. It is perhaps the simplest possible of the growing class of 4DVAR wind retrievals. It is Lagrangian in nature and considers the motion of individual air parcels initially collocated with analysis grid points. The sum of the forces acting on the parcels are assumed to be constant during an assimilation window consisting of just a few radar scans. These forces are unknown and must be retrieved along with the initial cross-beam wind component for each air parcel (i.e., for each analysis point). The retrieval consists of finding the initial cross-beam (azimuthal) wind component and forces for each parcel such that the difference between the predicted radial wind and the observed radial wind along a trajectory is minimized over the assimilation window. It can be performed with equal ease on a Cartesian or cylindrical grid. Conceptually, this algorithm is reminiscent of the Xu et al. (1994b, 1995) simple-adjoint retrievals (with provision for source terms in the equation of motion) and the Laroche and Zawadzki (1994, 1995) retrievals (which are cast in a semi-Lagrangian framework).

$\begin{displaymath} \frac{du}{dt}~=~a,~~~~~\frac{dv}{dt}~=~b.~~~~~~~~~~(4.1)\end{displaymath}$

Integrating (4.1) with respect to time (following the motion of the parcel) yields,

An expression for the radial coordinate of the parcel, r² = x² + y², follows from (4.4) and (4.5) and the relations, r₀v_r0 = x₀u₀ + y₀v₀, and u²₀ + v²₀ = v²_r0 + $v^{2}_{{\phi}0}$ (where r₀, v_r0 and $v_{{\phi}0}$ are the initial radial coordinate, radial velocity and azimuthal velocity, respectively):

$\begin{displaymath} r^{2}~=~\frac{1}{4}(a^{2}+b^{2})t^{4} + (au_{0}+bv_{0})t^{3}... ...i}0}+ax_{0}+by_{0})t^{2} + 2r_{0}v_{r0}t + r^{2}_{0}.~~~~~(4.6)\end{displaymath}$

From geometrical considerations, (and the convention that 0 $\deg$ corresponds to due north), the azimuthal coordinate of the parcel is found to be,

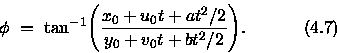
$\begin{displaymath} \phi~=~{\tan}^{-1}\Bigg(\frac{x_{0}+u_{0}t+at^{2}/2}{y_{0}+v_{0}t+bt^{2}/2}\Bigg).~~~~~~~~~~(4.7)\end{displaymath}$

Taking d/dt of (4.6) and noting that dr/dt = v_r, we obtain the predicted parcel radial velocity as,

$\begin{displaymath} rv_{r}~=~\frac{1}{2}(a^{2}+b^{2})t^{3} + \frac{3}{2}(au_{0}+... ...2}_{r0}+v^{2}_{{\phi}0}+ax_{0}+by_{0})t + r_{0}v_{r0}~~~~~(4.8)\end{displaymath}$

Equation (4.8) together with Eqs. (4.4) and (4.5) (for a Cartesian grid) or Eqs. (4.6) and (4.7) (for a cylindrical grid) form the basis of our new retrieval algorithm. The initial velocity components u₀ and v₀ appearing in (4.4) - (4.8) can be written in terms of the (known) initial radial wind component, v_r0, and the (unknown) initial azimuthal wind component, $v_{{\phi}0}$ :

$\begin{displaymath} u_{0}~=~{\sin}{\phi}_{0}v_{r0} + {\cos}{\phi}_{0}v_{{\phi}0},\end{displaymath}$

$\begin{displaymath} v_{0}~=~{\cos}{\phi}_{0}v_{r0} - {\sin}{\phi}_{0}v_{{\phi}0}.\end{displaymath}$

We consider a set of parcels such that each parcel is collocated with an analysis grid point at the intial time t = 0. For a given set of provisional or ``test'' values of a, b and $v_{{\phi}0}$ , the air parcel follows the test trajectory x(t), y(t) specified by (4.4) and (4.5), or, equivalently, the test trajectory r(t), ${\phi}(t)$ specified by (4.6) and (4.7). In either case, the test radial velocity v_r(t) for the parcel is specified by (4.8). At the radar's m'th volume scan time t_m we can compare the parcel's test radial velocity v_r(t_m) with the observed value of v_r interpolated to the test location x(t_m), y(t_m) (or, equivalently, to r(t_m), ${\phi}(t_{m})$ ). Our retrieval should determine the a, b and $v_{{\phi}0}$ that yield the best agreement between the observed and test values of v_r over a window of observation times. Toward that end, we seek to minimize a cost-functional (error functional) J defined as the sum of the (squared) differences,

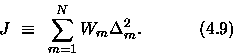
$\begin{displaymath} J~\equiv~\sum_{m=1}^{N}W_{m}{\Delta}^{2}_{m}.~~~~~~~~~~(4.9)\end{displaymath}$

$\begin{displaymath} {\Delta}_{m}~\equiv~\{rv_{r}\}_{m} - \frac{1}{2}(a^{2}+b^{2}... ...{m} - \frac{3}{2}(au_{0}+bv_{0})t^{2}_{m} - r_{0}v_{0},~~(4.10)\end{displaymath}$

$\begin{displaymath} \{rv_{r}\}_{m}~\equiv~rv_{r}(x(t_{m}), y(t_{m}), t_{m}),\end{displaymath}$

$\begin{displaymath} \{rv_{r}\}_{m}~\equiv~rv_{r}(r(t_{m}), {\phi}(t_{m}), t_{m}).\end{displaymath}$

In principle, the minimization of J (which determines the optimal set of parameters a, b and $v_{{\phi}0}$ ) can be accomplished by finding the path of steepest descent down the $J(a, b, v_{{\phi}0})$ topography from a point corresponding to an initial guess of a, b, $v_{{\phi}0}$ . However, in the present version of the retrieval code we minimize J by ``brute force,'' that is, by explicitly evaluating J for a volume of a, b, $v_{{\phi}0}$ values and selecting the triple of values that yield the smallest local minimum in J. Although time-consuming, this approach is desirable for our preliminary ``research mode'' experiments because it provides us with a valuable diagnostic tool: a global view of the J topography. By revealing the distribution of possible multiple minima, such a view may facilitate insights into the nature of solution nonuniqueness.

The retrieval was tested on a cylindrical grid with three successive volume scans of WSR-88D Doppler radar data gathered at 6 minute intervals from the KTLX site near Norman, Oklahoma. The first time level was 1756 UTC. The reflectivity field at z = 5.25 km (Fig. 2) shows a squall line passing eastward through central Oklahoma. The corresponding dual-Doppler analyzed wind vectors obtained with data from the KTLX radar and the nearby Cimarron Doppler radar are shown in Fig. 3. On the whole, the retrieved wind vectors at z = 5.25 km (Fig. 4) are in good agreement with the dual-Doppler winds (Fig. 3). Results from the corresponding two-scalar retrieval (described in section 3) are shown in Fig. 5.

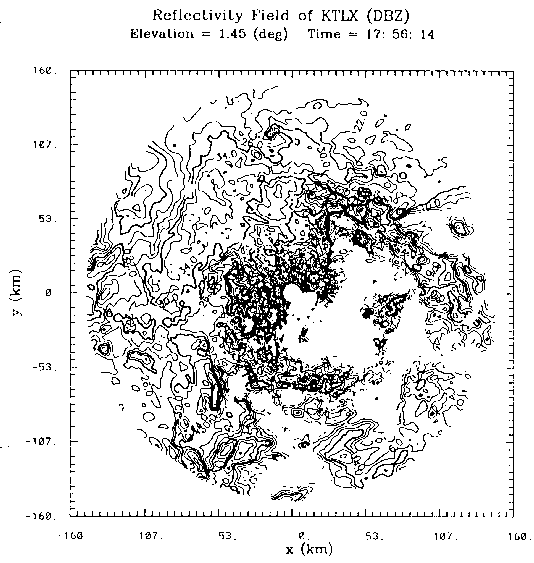$\begin{figure} \par \centerline{ \psfig {file=Fig2.ps,height=6in} } \par\end{figure}$

Fig. 2. Low level reflectivity (dBZ) at 1756 UTC from the KTLX radar for 7 May 1995 squall line. $\theta$ = 1.45 $\deg$ .

$\begin{figure} \par \centerline{ \psfig {file=Fig3.ps,height=6in} } \par\end{figure}$

Fig. 3. Dual-Doppler analyzed wind vectors at z = 5.25 km for 7 May 1995 squall line.

$\begin{figure} \par \centerline{ \psfig {file=Fig4.ps,height=6in} } \par\end{figure}$

Fig. 4. Retrieved wind vectors at z = 5.25 km from the new 4DVAR method for 7 May 1995 squall line.

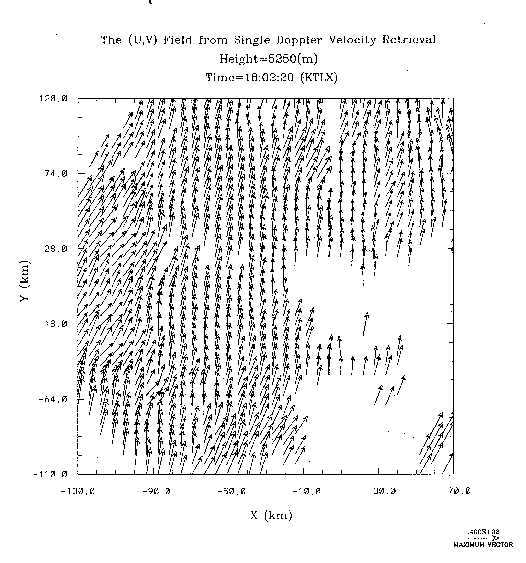$\begin{figure} \par \centerline{ \psfig {file=Fig5.ps,height=6in} } \par\end{figure}$

Fig. 5. Retrieved wind vectors at z = 5.25 km from the two-scalar Shapiro et al. (1995a) method for the 7 May 1995 squall line.

5. Initial forecast fields created from SDVR winds, thermodynamic retrieval and an analysis package, ADAS.

The primary research tool for this exercise is an assimilation procedure consisting of the Advanced Regional Prediction System (ARPS), the ARPS Data Analysis System (ADAS) and single-Doppler velocity retrieval and thermodynamic retrieval modules. Taken together, this comprises the current version of the ARPS single-Doppler ingest/retrieval system.

In the following sub-sections we will describe the impact of single-Doppler radar data and single-Doppler retrieved fields on both the analysis and subsequent model prediction of an Oklahoma squall line. The initialization takes place at a time when strong convec-tion is already occuring in the analysis domain, and thus represents an exercise in reducing the spin-up time for model convection rather than an attack on the convec-tive initiation problem.

The initialization begins by estimating the cross-beam winds from single-Doppler data on a spherical grid following the previously described algorithm of Shapiro et al. (1995a). These retrieved winds are then blended with ADAS-analyzed background fields on a Cartesian grid. Following a wind-adjustment step in which the winds are forced to satisfy the anelastic mass conservation equation on a Cartesian grid, the Gal-Chen (1978) thermodynamic retrieval is applied. Theretrieved wind and thermodynamic data are then treated as pseudo-observations (``bogus'' data) in an ADAS reanalysis. Although this constructive procedure is not particularly elegant, it is perhaps the simplest means of integrating radar data and radar derived fields into a numerical model, and is therefore appropriate for proof-of-concept studies related to the impact of radar data in numerical weather prediction models. The steps in this procdure are summarized schematically in Fig. 6.

$\begin{figure} \par \centerline{ \psfig {file=Fig6.ps,height=6in} } \par\end{figure}$

Fig. 6. Flow chart illustrating one cylce of the forward radar-data assimilation procedure.

Experiments with this procedure were conducted with Level II KTLX (Twin Lakes, Oklahoma) WSR-88D Doppler radar data gathered on the afternoon of 7 May 1995. Two squall lines crossed Oklahoma on this day, one of which produced a tornado in the city of Ardmore, Oklahoma. Initialization occurs while the first squall line is moving eastward through central Oklahoma. Experiments were performed with the same grid configuration used during the 1996 spring realtime operational period (Droegemeier et al. 1996, Xue et al. 1996b), but also incorporated the full single-Doppler retrieval procedure described here. Our experiments focused on the first line as it passed through central Oklahoma, and consisted of a 3-hour forecast initialized at 1800 UTC. The radar reflectivity field from the KTLX radar at 1756 UTC is shown in Fig. 2. The individual components comprising this analysis/prediction system are now described.

The thermodynamic retrieval step and the model prediction are performed with the Advanced Regional Prediction System (ARPS). The ARPS governing equations are three-dimensional, non-hydrostatic and fully compressible. They are solved on an Arakawa C grid with a split-explicit (mode-splitting) solution technique in which the acoustic modes are explicitly integrated with a forward-backward scheme on small time steps. The equations are discretized with second-order centered spatial differences and integrated on big time steps with the leapfrog scheme (and a Robert-Asselin time filter). A complete description of the model, including the governing equations, initialization, boundary condition options, discretizations and numerical solution techniques can be found in the ARPS User's Guide (1995).

ADAS (Brewster 1996) is an analysis package developed for the ARPS model which can incorporate conventional observational data (e.g., surface, mesonet, rawinsonde) as well as data from Doppler radars and radar-derived data. ADAS is based on the Bratseth technique (Bratseth 1986), a successive correction approximation to Optimal Interpolation. The implementation adopted for this work uses analyzed data from the Rapid Update Cycle (RUC) (Benjamin et al. 1994) as background fields.

This retrieval (discussed in section 3) requires three successive time levels of radar data to obtain wind estimates at one time level. Since three time levels of wind estimates are required for application of the Gal-Chen (1978) thermodynamic retrieval, the retrieval was applied three times in succession, requiring five time levels of radar data. The retrieval results were validated at the central time with a dual-Doppler analysis performed with data from the KTLX and Cimarron Doppler radars. The retrieved and dual-Doppler analyzed wind vectors at z = 5.25 km have already been displayed in Figs. 5 and 3, respectively. One notes a good qualitative agreement between the retrieved and dual-Doppler vectors at this level. However, wind vectors at other levels were not as impressive. It should also be noted that much of the horizontal convergence in this case is due to convergence in the radial direction, which is obtained directly from the radar measurements.

The single-Doppler retrieved winds are obtained on a spherical grid, whereas the thermodynamic retrieval (which will utilize these winds) has been coded up in its simplest form, that is, on a Cartesian grid. We must therefore interpolate the retrieved winds to Cartesian grid points. We combine this step with a simple blend (using optimum interpolation) using ADAS background winds of 5 km resolution. In areas where radar data (and retrieved fields) are not available, ``bogus'' hole-filled fields were created by applying the two-dimensional Laplace equation to the data voids given ADAS fields as boundary conditions.

In order to insure that the analyzed winds satisfy the mass conservation constraint on the Cartesian grid, we made use of a variational wind adjustment step patterned on the technique of Liou et al. (1991), but modified to take into account the spherical nature of the radar observation (Shapiro et al., 1995c). The velocity vectors obtained from the variational adjustment step are such that their projection in the direction of the Doppler radar agrees with the radial wind observations while anelastic mass conservation is satisfied on the model grid and departures from the first guess wind field are minimized. The minimization is obtained by solving the relevant Euler-Lagrange equations.

The ARPS thermodynamic retrieval is based on the Gal-Chen (1978) procedure, which determines the pressure field from the requirement that it satisfy, in a least squares sense, the horizontal equations of motion with the (known) velocity-dependent forcings. The evaluation of these velocity-dependent terms utilizes the variationally-adjusted winds described above. Specific-ally, the variationally-adjusted winds are quadratically interpolated from three consecutive radar observation times to three consecutive model times centered on the time of thermodynamic retrieval. These interpolated winds are then used to evaluate the advection, turbulence, Coriolis force and computational mixing terms in the model equations of motion (using the model subroutines). The local derivative terms are discretized with centered time differences on the model time steps.

The least squares formulation leads to a two-dimensional Poisson equation for the pressure, which may be conveniently solved with a standard SOR algorithm. In contrast to the traditional thermodynamic retrieval method which uses Neumann boundary conditions, we make free use of ADAS boundary data to supply Dirichlet conditions. The advantages of this approach are that (i) ADAS pressure data are incorporated in the solution and (ii) the solution is unique (unlike the traditional formulation where the solution contains an arbitrary function of height).

It is important to note that the forcing terms in the Poisson equation were only trusted in the region where there was originally radar reflectivity data. Outside of the reflectivity area, the forcing terms were set to zero, and the Poisson equation reduced to a two-dimensional Laplace equation. Since the pressure field satisfies Laplace's equation outside the reflectivity area, it is characterized by the same features as other harmonic functions: it is the solution of minimum (least squares) gradient, and extrema are limited to the boundaries of the domain (i.e., the exterior computational boundaries and the interior boundaries defined by the data/no-data interface).

Once the pressure has been recovered, the buoyancy is obtained as a residual from the vertical equation of motion. In order to account for the presence of moisture fields in the buoyancy term, we use radar reflectivity data as proxies for the rainwater and (indirectly) water vapor fields.

Following the thermodynamic retrieval step, the retrieved wind and thermodynamic data are treated as pseudo-observations in the ADAS reanalysis step. Specifically, these fields are treated as sounding data where radar data are originally available. In this manner information about the wind and thermodynamic fields obtained from radar data is incorporated into the initial state of the model grid.

We describe two experiments: (1) a control run in which no radar data or radar-derived fields are used and (2) a run utilizing the radar data and retrieved fields following the prescription described above. In both cases the computational domain consisted of a fine grid (dx = 3 km) covering 300 x 300 km² nested within a coarse grid (dx = 9 km) covering 900 x 900 km². RUC forecast fields were used as boundary conditions in both runs. In the radar data experiment, five consecutive scans of KTLX data (at six minute intervals) were used to create single-Doppler retrieved winds at three consecutive time levels. These retrieved data and ADAS background fields were then used to retrieve the thermodynamic fields at the middle time level (see Fig. 6).

The impact of the radar data is particularly notable two hours into the forecast, at 2000 UTC. Fig. 7 depicts the observed reflectivity field at 2000 UTC. Fig. 8 depicts the corresponding control-run forecast reflectivity field (really rainwater converted to reflectivity through a semi-empirical relation) and wind vectors at z = 2 km. Fig. 9 depicts the corresponding forecast fields from the experiment with ingested radar data. The main differences between the control run (Fig. 8) and the run with radar data (Fig. 9) appear in northern Oklahoma. Comparing the predicted reflectivities with the observations (Fig. 7), we see that the areal coverage and intensity of the precipitation in northern Oklahoma is reasonably well forecast in the radar data run but not in the control run. The location of the improvement suggests that convective elements initialized from the single-Doppler radar data may have been advected northward by the strong mid-tropospheric southerly winds. By three hours (not shown), these storms had moved northward out of the domain, and the control run and experiment were fairly similar.

$\begin{figure} \par \centerline{ \psfig {file=Fig7.ps,height=6in} } \par\end{figure}$

Fig. 7. Low level reflectivity (dBZ) at 2000 UTC from the KTLX radar for 7 May 1995 squall line.

$\begin{figure} \par \centerline{ \psfig {file=Fig8.ps,height=6in} } \par\end{figure}$

Fig. 8. 2000 UTC predicted wind vectors and reflectivity field at z = 2 km for the control run.

$\begin{figure} \par \centerline{ \psfig {file=Fig9.ps,height=6in} } \par\end{figure}$

Fig. 9. 2000 UTC predicted wind vectors and reflectivity field at z = 2 km for run with radar data.

Further exploration of this case revealed that the improvement in the forecast with the radar data was directly due to the combined effects of the derived thermodynamic information and the derived water vapor information, rather than to the wind field information per se. On the other hand, the wind field was required to obtain the thermodynamic information.

The preceding discussion of wind retrieval tech-niques and radar data assimilation is in no way intended to be complete. We have not discussed any of the results pertaining to error analyses. Neither have we discussed the prospect of using radar data in assimilation ``cycles'' or the use of 4DVAR approaches involving the full equation set of a nonlinear weather prediction model. Both ``simple'' and ``sophisticated'' approaches have their own set of theoretical and practical difficulties that, for the most part, have limited their usage to simulated data or research mode experiments with real data. However, the preliminary results produced in this new field suggest a potential for useful information to be extracted from single-Doppler radar data. These retrievals may prove to be useful tools in their own right as well as ``adding value'' to storm-scale numerical model forecasts.

This research was supported by the Center for Analysis and Prediction of Storms (CAPS) at the University of Oklahoma under Grant ATM91-20009 from the National Science Foundation (NSF), by the Federal Aviation Administration (FAA) under grant ATM-8809862, and by the United States Department of Defense (Navy) under Grant N00014-96-1-1112. The author is indebted to Limin Zhao, Yidi Liu, Steve Lazarus, Steve Weygandt and Scott Ellis for their assistance with the research described herein. Sue Weygandt assisted with the figure preparation.

Benjamin, S. G., K. J. Brundage, P. A. Miller, T. L. Smith, G. A. Grell, D. Kim, J. M. Brown, T. W. Schlatter, and L. L. Morone, 1994: The Rapid Update Cycle at NMC. Preprints, 10th Conf. on Numerical Weather Prediction, Portland, OR, Amer. Meteor. Soc., 566-568.

Bratseth, A. M., 1986: Statistical interpolation by means of successive corrections. Tellus, 38A, 439-447.

Brewster, K., 1996: Application of a Bratseth analysis scheme including Doppler radar data. Preprints, 15th Conf. on Weather Analysis and Forecasting, Norfolk, VA, Amer. Meteor. Soc., 92-95.

Droegemeier, K. K., M. Xue, K. Brewster, Y. Liu, S. K. Park, F. Carr, J. Mewes, J. Zong, A. Sathye, G. Bassett, M. Zou, R. Carpenter, D. McCarthy, D. Andra, P. Janish, R. Graham, S. Sanielvici, J. Brown, B. Loftis, and K. McLain, 1996: The 1996 CAPS spring operational forecasting period: Realtime storm-scale NWP, Part I: Goals and methodology. Preprints, 11th Conf. on Numerical Weather Prediction, Amer. Meteor. Soc., Norfolk, VA, 294-296.

Gal-Chen, T., 1978: A method for the initialization of the anelastic equations: Implications for matching models with observations. Mon. Wea. Rev., 106, 587-606.

Gal-Chen, T., 1982: Errors in fixed and moving frame of references: Applications for conventional and Doppler radar analysis. J. Atmos. Sci., 39, 2279-2300.

Kapitza, H., 1991: Numerical experiments with the adjoint of a nonhydrostatic mesoscale model. Mon. Wea. Rev., 119, 2993-3011.

Koscielny, A. J., R. J. Doviak, and R. Rabin, 1982: Statistical considerations in the estimation of divergence from single-Doppler radar and application to prestorm boundary-layer observations. J. Appl. Meteor., 21, 197-210.

Laroche, S., and I. Zawadzki, 1994: A variational analysis method for retrieval of three-dimensional wind field from single Doppler radar data. J. Atmos. Sci., 51, 2664-2682.

Laroche, S., and I. Zawadzki, 1995: Retrievals of horizontal winds from single-Doppler clear-air data by methods of cross-correlation and variational analysis. J. Atmos. Oceanic Technol., 12, 721-738.

Lhermitte, R. M. and D. Atlas, 1961: Precipitation motion by pulse Doppler radar. Preprints, 9th Weather Radar Conf., Kansas City, Amer. Meteor. Soc., 218-223.

Liou, Y. C., T. Gal-Chen, and D. K. Lilly, 1991: Retrievals of wind, temperature and pressure from single-Doppler radar and a numerical model. Preprints, 25th Intl. Conf. on Radar Meteor., Paris, France, Amer. Meteor. Soc., 151-154.

Qiu, C.-J., and Q. Xu, 1992: A simple adjoint method of wind analysis for single-Doppler data. J. Atmos. and Oceanic Technol., 9, 588-598.

Rinehart, R. E., 1979: Internal storm motions from a single non-Doppler weather radar. NCAR/TN 146+STR, 262 pp.

Shapiro, A., S. Ellis, and J. Shaw, 1995a: Single-Doppler velocity retrievals with Phoenix II data: Clear air and microburst wind retrievals in the planetary boundary layer. J. Atmos. Sci., 52, 1265-1287.

Shapiro, A., T. Gal-Chen, J. Zhang, L. Zhao, Q. Xu, H. Gu, C.-J. Qiu, I. Zawadzki, S. Laroche, and J. Tuttle, 1995b: Highlights from a single-Doppler velocity retrieval intercomparison project. Preprints, 6th Conf. on Aviation Weather Systems, Dallas, TX, Amer. Meteor. Soc., 541-546.

Shapiro, A., K. K. Droegemeier, S. Lazarus, and S. Weygandt, 1995c: Forward variational four-dimensional data assimilation and prediction experiments using a storm-scale numerical model. Preprints, International Symposium on Assimilation of Observations in Meteorology and Oceanography, Tokyo, Japan. WMO, 361-366.

Sun, J., D. W. Flicker, and D. K. Lilly, 1991: Recovery of three-dimensional wind and temperature fields from simulated Doppler radar data. J. Atmos. Sci., 48, 876-890.

Sun, J., and N. A. Crook, 1994: Wind and thermo-dynamic retrieval from single-Doppler measurements of a gust front observed during Phoenix II. Mon. Wea. Rev., 122, 1075-1091.

Tuttle, J. D., and G. B. Foote, 1990: Determination of the boundary layer airflow from a single Doppler radar. J. Atmos. and Oceanic Technol., 7, 218-232.

Waldteufel, P. and H. Corbin, 1979: On the analysis of single-Doppler radar data. J. Appl. Meteor., 18, 532-542.

Weygandt, S., A. Shapiro, and K. K. Droegemeier, 1995: Adaptation of a single-Doppler velocity retrieval algorithm for use on a deep-convective storm. Preprints, 27th Conf. on Radar Meteorology, Vail, CO, Amer. Meteor. Soc., 264-266.

Xu, Q., C. J. Qiu, and J.-X. Yu, 1994a: Adjoint-method retrievals of low-altitude wind fields from single-Doppler reflectivity measured during Phoenix-II. J. Atmos. Oceanic Technol., 11, 75-288.

Xu, Q., C. J. Qiu, and J.-X. Yu, 1994b: Adjoint-method retrievals of low-altitude wind fields from single-Dopper wind data. J. Atmos. Oceanic Technol., 11, 579-585.

Xu, Q., C. J. Qiu, H.-D. Gu, and J.-X. Yu, 1995: Simple adjoint retrievals of microburst winds from single-Doppler radar data. Mon. Wea. Rev., 123, 1822-1833.

Xue, M., K. K. Droegemeier, V. Wong, A. Shapiro and K. Brewster, 1995: ARPS Version 4.0 Users' Guide. Center for Analysis and Prediction of Storms. Univ. of Oklahoma. 381 pp.

Xue, M., K. K. Droegemeier, D. Wang, and K. Brewster, 1996a: Prediction and simulation of a squall line case during VORTEX-95. Preprints, 18th Conf. on Severe Local Storms, San Francisco, Amer. Meteor. Soc., 169-173.

Xue, M., K. Brewster, K. K. Droegemeier, V. Wong, D. H. Wang, F. Carr, A. Shapiro, L. Zhao, S. Weygandt, D. Andra, and P. Janish, 1996b: The 1996 CAPS spring operational forecasting period: Realtime storm-scale NWP, Part II: Operational summary and sample cases. Preprints, 11th Conf. on Numerical Weather Prediction, Amer. Meteor. Soc., Norfolk, VA, 297-300.

Zawadzki, I. I., 1973: Statistical properties of precipitation patterns. J. Appl. Meteor., 12, 459-472.

Zhang, J., and T. Gal-Chen, 1996: Single-Doppler wind retrieval in the moving frame of reference. J. Atmos. Sci., 53, 2609-2623.