In the context of 3-D models, the number of IVs is potentially very large when grid variables are considered, and this may inhibit the practical computation of sensitivity because of memory limitations. We propose to compute sensitivities with respect to the perturbations inserted in model variables rather than the grid variables themselves. That is, by introducing an artificial perturbation parameter, e, into the original forward model (ARPS), ADIFOR can generate a sensitivity code that regards e as one of the IVs [5].
Consider, for
example, the water vapor field, 
. If we perturb it by a factor e,
any quantity P that is influenced by the water vapor field implicitly depends upon e. Expanding P(e) in a Taylor series about the reference state [P(e = 0)] and retaining only the first-order term, we obtain an approximation of the sensitivity of P with respect to e:
Here, 
can be interpreted as the sensitivity of P to a uniform
relative change in the water vapor field. We have modified the ARPS to
include e as an input parameter, as shown in (1), and have applied
ADIFOR to differentiate this code with respect to e.
Since the perturbation e is added to the input parameters, which already have their own characteristic distribution in the model domain, sensitivities computed from this approach implicitly involve the effect of distribution for those parameters. We limit our experiments only to initial conditions. Boundary conditions, including lateral, top, and bottom, are excluded for sensitivity experiments and TLM validation.
We also compute
sensitivities of the cost function with respect to perturbations in all
forecast aspects. The cost function, J, is defined as the squared
distance between the model state, 
, and the corresponding observations,
:
where 
denotes a scalar product between
and 
and n represents
the time index.
Here, the scalar product
implies the sum of the products of corresponding components of the
two vectors [9].
is a weighting factor matrix, where = 
for the 3-D ARPS with subscripts
corresponding to model variables,
where u, v, and w are the
Cartesian components of velocity, 
is the potential temperature, p is the
pressure, , 
and 
are mixing ratios of water vapor,
cloud water, and rain
water, respectively.
The weight for the vertical velocity,
, for example, is computed following Wang [20],
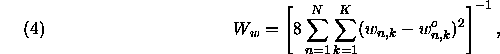
with similar expressions for other variables. Here, k denotes the grid space index. In this manner, the cost function is nondimensionalized and becomes unity at the beginning of the variational data assimilation window.