6. Sensitivity Results

We now investigate the effect of perturbations introduced in the water vapor field in different regions of storm environments on storm dynamics. The water vapor field is a major factor for storm life and morphology. We introduce four perturbation equations following the equation (1) for four different regions in the model: ( ) inside the rain region ( ) above the cloud base, ( ) in the ambient environment outside the rain region and above the cloud base, ( ) the updraft region (including w = 0) in the subcloud layer, and ( ) the downdraft region in the subcloud layer. For the cost function, sensitivities are computed for perturbations in all forecast aspects (i.e., ) both inside and outside the rain region of the storm.

To investigate the sensitivity of our storms to perturbations in the water vapor, we run the SE-ARPS starting at 50 min, i.e., the effect of the perturbation begins when the storm is in its developing stage, see Figure 1a. Among the many available results, we investigate the sensitivity of ground rainfall (GR) to water vapor perturbations in the four regions described above.

The cloud base at 50 min is around 640 m. Four model levels are involved in the subcloud layer (excluding the bottom boundary). The numbers of grid points involved in perturbation are 8280 for , 61720 for , 5972 for , and 4028 for .

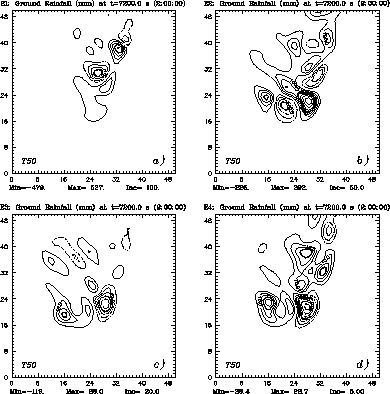
The amount and location of ground rainfall are among the most important quantities in storm-scale prediction. Figure 3 shows the sensitivity of GR at 120 min with respect to the previous four perturbations inserted at 50 min. Recall that, at 120 min, the main updraft is located near the center of the domain with a lima-bean shape, while a secondary storm develops to the west (see Figure 1b). Also, a prominent secondary storm exists to the northeast of the main storm, along with another weak storm near the northern lateral boundary.

Among all perturbations, the largest sensitivity of GR is due to the perturbation. For vapor perturbations inside the rain region ( ), the major increase in GR occurs in the secondary storm with a maximum of 527 mm (Figure 3a). The GR decreases at the weak downdraft region to the north of the main storm with a minimum of -479 mm. This indicates that a 1% moisture perturbation inside the rain region above the cloud base at t = 50 min induces a maximum increase of 5.27 mm and a decrease of 4.79 mm in the secondary storm rainfall at t = 120 min.

The major influence of the perturbation occurs in the main storm area, with a large increase beneath the main storm and a decrease in the western part and north of the storm (Figure 3b). Both the and perturbations result in a decrease below the main storm and increase below the secondary storm in the west (Figures 3c and 3d). The sensitivity to the perturbation is about three times larger than that to the perturbation. The perturbation also increases GR at the region of north secondary storm.

Overall, the largest influence on GR comes from the perturbation, but at the secondary storm to the north. For the main storm, while the moisture perturbation in the ambient environment above the cloud base ( ) increases the ground rainfall, the perturbations in both the updraft and downdraft region below the cloud base ( and ) decrease the ground rainfall at 120 min.

 

Figure 3: Sensitivities of ground rainfall at t = 120 min with respect to the moisture perturbations of (a)

, (b)

, (c)

and (d)

at t = 50 min (in mm)

We now discuss the sensitivity results in the cost function and their implications on data assimilation. We consider the control simulation (see Figure 1) as our pseudo-observations. The sensitivity period is 30 min, from t = 80 min to t = 110 min. A 1% perturbation is added to all variables at all grid points at 80 min for the perturbation run, which serves as the nonlinear basic field for the sensitivity computation.

With this perturbation, model solutions show little difference from the observations. Note that ARPS actually predicts the perturbations of potential temperature ( ) and pressure (p). Since the total fields of and p are observed in practice (i.e., base state + perturbation), we specify their total fields as independent variables for the sensitivity computation rather than using the perturbation fields.

The weight functions computed from (4) for this experiment are , , , , , , = 14.36 , and = 0.87 . As defined in (4), the weight function of any variable is inversely proportional to the amount of forecast error in that variable, which is summed from the perturbation insertion time to the verification time.

In Table 1, we show the adjoint sensitivities of the cost function (J) at 110 min to perturbations at 80 min in specified variables both inside (IN) and outside (OUT) the rain region. Because they are nondimensional and the cost function is unity at this time (110 min), we can compare the relative importance among variables.

 

Table 1: Sensitivity of cost function at 110 min with respect to the perturbations of forecast aspects at 80 min both inside (IN) and outside (OUT) the rain region

For the perturbations inside the rain region, the largest sensitivity in the cost function (i.e., forecasting error) is due to errors in potential temperature ( ), followed by pressure (p) and water vapor ( ). The sensitivities are positive for all three perturbations. Among all variables, the cloud water ( ) perturbation exerts the smallest effect on the cost function. Among the moisture variables inside the cloud, water vapor exerts the largest influence on J, followed by rainwater ( ) and cloud water.

Perturbations in the momentum variables (u, v and w) inside the rain region yield small changes in J. Among them, the largest sensitivity of J is due to the v perturbation, and the smallest is due to the u perturbation. For perturbations outside the rain region, the sensitivities are generally smaller than those for perturbations inside the rain region, except for the sensitivity to the u perturbation. Note the prominent decrease in the influence on J of perturbations in p. Since and are effectively zero in the environment, the sensitivities of J to them are extremely small. The largest sensitivity in the cost function is due to , followed by and p.

The perturbations in , and v outside the rain region induce similar changes in J, but in different directions compared with those inside the rain region. Other variables demonstrate significant changes in sensitivity values. For example, the absolute sensitivity of the cost function to the u perturbation outside the rain region is about 100 times larger than inside the rain region, while the sensitivity to the perturbation is about 1.2 times larger.

In both cases, the p field has the largest effect on the cost function during the early sensitivity period (not shown). This is because p is directly responsible for the mass balance through the pressure gradient forces in the momentum equations. When p is perturbed, the flow accelerates until terms involving the velocity become comparable with the pressure gradient force. Therefore, the flow immediately and significantly responds to the p perturbations. In contrast, perturbations in affect the system initially through only buoyancy term in the vertical momentum equation. That is, p affects all three components of velocity simultaneously through the pressure gradient force, while affects only the vertical velocity initially and then other variables through mass continuity. Hence, during the early sensitivity period, the p perturbations exert the largest influence on forecast errors among all variables. However, the increased buoyancy through the perturbation eventually influences storm dynamics and forecast error.